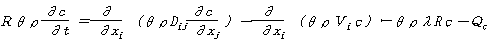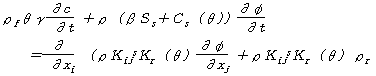大気・水・環境負荷分野の環境影響評価技術検討会中間報告書
大気・水・環境負荷分野の環境影響評価技術（I）＜スコーピングの進め方＞（平成12年8月）

大気・水・環境負荷分野の環境影響評価技術（I）TOPへ戻る

技術シート　登録番号：地下水－10

環境項目 地下水 技術等の種類 予測
技術等の名称 数値解析モデル：移流・分散モデル
技術等の概要 物質輸送モデルは、大きく流動方程式と移流分散方程式から構成される。流動方程式を解くことにより地下水位分布を求め、ダルシーの法則を適用して地下水流速の分布を算出する。算出した流速分布を移流分散方程式及び浸透方程式に入力して解くことで、濃度分布が求められる。
　解析手法としては、[1]粒子追跡法、[2]オイラー法、[3]オイラリアン・ラグランジアン法（EL法）、[4]LTG法等がある。
（移流分散方程式）

fig_03.gif (808 バイト)

ここで、

Ｒ：遅延係数、Dij：分散テンソル、Ｖi；実流速、Ｑc ：源泉項（解析対象地域内での揚水・注水項）、θ：体積含水率、ρ：流体の密度、λ：減衰定数、ｃ：濃度、ｔ：時間

（浸透方程式）

fig_04.gif (1032 バイト)

ここで、

ψ：圧力水頭、Ｓs：比貯留係数、Ｃs（θ）：比水分容量、Ｋijs：飽和透水テンソル、Ｋr（θ）：比透水係数、ρf：水溶媒の密度、ρ：流体の密度、ρr：溶媒の密度（ρf）に対する流体の密度比（＝ρ/ρf）、β：飽和領域でβ＝1，不飽和領域でβ＝0、γ：溶質の密度比
調査・予測の
必要条件		 1．解析に必要な物理特性

（移流分散解析） （浸透解析）
・縦分散長（αL） ・飽和透水係数（Ｋs）
・横分散長（αT） ・比貯留係数（Ｓs）
・分子拡散係数（αm） ・間隙率（ｎ）
・屈曲率（τ） ・不飽和領域のｐＦ曲線（水分特性曲線）
・吸着係数（Ｋd） ・不飽和透水係数（Ｋ－θ）
・減衰係数（λ）

2．解析に必要な条件
1）境界条件
・移流分散解析：濃度既知境界、流量既知境界
・浸透解析：圧力水頭既知境界、流量既知境界

2）初期条件
・移流分散解析：初期状態における濃度の平面・断面分布
・浸透解析：地盤内の水位と深さ方向の水圧分布、不飽和領域の飽和度の分布、負の圧力水頭（サクション）の現状分布

環境項目 地下水 技術等の種類 予測
技術等の名称 数値解析モデル：移流・分散モデル
適用範囲 ・均質多孔体の飽和・不飽和領域に適用。
課題 　実際のフィールドは不均質であるため、フィンガー状の不均質な汚染パターンが生じ、移流・拡散式の適用は限定される。
参考とした
文献・資料		 西垣　誠（1998）地下水汚染の解析．地質と調査、3、21-27．
地下水ハンドブック編集委員会（1998）改訂地下水ハンドブック．(株)建設産業調査会、東京、pp1504．
地下水の科学研究会（1995）地下水の科学I．土木工学会、東京、pp235．
地下水の科学研究会（1996）地下水の科学II．土木工学会、東京、pp252．
地下水の科学研究会（1996）地下水の科学III．土木工学会、東京、pp194．
備考

前ページへ　次ページへ