大気・水・環境負荷分野の環境影響評価技術検討会中間報告書
大気・水・環境負荷分野の環境影響評価技術(II)<環境影響評価の進め方>(平成13年9月)
大気・水・環境負荷分野の環境影響評価技術(II)TOPへ戻る
技術シート 登録番号:振動-1
| 環境項目 | 振動 | 技術等の 種類 |
予測 |
|---|---|---|---|
| 技術等の名称 | 建設省土木研究所提案式(道路交通振動の予測) | ||
| 技術等の概要 | 建設省土木研究所提案式は、自動車1台走行時の地盤振動値を設定し、交通流の発生にシミュレーションを用い、交通量、路面平坦性及び地盤条件等から回帰分析手法を用いて、予測式の各種補正項を設定した式である。
【予測式】
ここで、 L10 :振動レベルの80%レンジの上端値の予測値(dB)
K :13(V≦100km/時)、14(V>100km/時) V :平均走行速度(km/時) M :上下車線合計の車線数
|
||
| 調査・対象の 必要条件 |
小型車および大型車の時間交通量
平均走行速度 上下線合計の車線数 地盤卓越振動数 道路構造 |
||
| 適用範囲 | 平面道路:等価交通量(600以下)、走行速度(20~100)、車線数(2~8)、路面平坦性(1~7mm)
高架道路:等価交通量(50~850)、走行速度(40~100)、車線数(2~8)、最大段差量(5~30mm) 盛土道路:盛土高さ(2~8.5m) 切土道路:切土深さ(2.5~10m) 掘割道路:掘割深さ(2~6m) |
||
| 課題 | ・
振動源と受振点に介在する媒質の変化量を考慮した予測の検討
・ 地盤性状を考慮した予測の検討 |
||
| 参考とした 文献・資料 |
建設省(1986)建設省庁所管道路事業環境影響評価に関する実施上の運用(案)について.
日本道路協会(1989)道路環境整備マニュアル.丸善、東京、pp257. |
||
| 備考 | |||
技術シート 登録番号:振動-2
| 環境項目 | 振動 | 技術等の 種類 |
予測 |
|---|---|---|---|
| 技術等の名称 | エネルギーベースの道路交通振動の予測 | ||
| 技術等の概要 | 東京都の地盤を対象に作成された式であり、建設省土木研究所提案式との主な相違点は以下のとおりである。
・ 地盤の種類を明確に分類していること(ローム、砂礫、沖積地盤) ・ 舗装構造を取り入れている
本式は振動加速度レベルのエネルギ―平均値(Leq)を求め、実験値のシミュレーション結果から求められた振動加速度レベルの80%レンジの上端値との関係式からL10を算出し、実測結果から求めた加速度レベルと振動レベルの差、ΔLから振動レベルを予測するものである。 本式では、振動加速度レベルのエネルギー平均値を算出することから、各車線からの振動を合成することが可能である。 |
||
| 調査・予測の 必要条件 |
走行速度、車両台数等 | ||
| 適用範囲 |
・ 地盤:ローム、砂れき、沖積地盤
・ 車線数:最大6車線 ・ 路面の平坦性:1~6mm ・ 等値換算総厚:10~60cm ・ 走行速度:20~70km/時 ・ 車両台数:(35台/10分~350台/分)/1車線 ・ 予測範囲:道路直角方向30mまで |
||
| 課題 | ・ 東京都の地盤上の平面道路が対象 | ||
| 参考とした 文献・資料 |
横田明則(1994)道路交通振動の予測.騒音制御、18(6)、300-303. | ||
| 備考 | |||
技術シート 登録番号:振動-3
| 環境項目 | 振動 | 技術等の 種類 |
予測 |
|---|---|---|---|
| 技術等の名称 | 回帰式による予測方法(地下鉄) | ||
| 技術等の概要 | トンネルからの距離(X)、トンネル重量(Y)、走行速度(Z)の各々の基準値に対する増減による振動レベルの増減を、軌道別の振動レベルの基準値Kに加えて、地表振動の予測値を求める方法である。
帝都高速度交通営団の提案式であるが、事例調査結果を用いて、K、X0、Y0、Z0を回帰分析より求め援用して用いられている。
予測の基本式: L=K-AlogX/X0-24logY/Y0+20logZ/Z0 A:地盤条件による決まる定数 L:鉄道振動レベル(dB) X:トンネルから予測地点までの距離 Y:1m当たりのトンネル重量(t/m) Z:走行速度(km/時) |
||
| 調査・予測の 必要条件 |
トンネル重量、走行速度、地盤性状等 | ||
| 適用範囲 | ・ 地下鉄トンネル近傍の地表振動レベルの予測。
・ 東京と近辺の一般的地盤を対象としたものである。 |
||
| 課題 | ・ 他地域で用いる場合は、その適用の妥当性を検証する必要がある。(特に土質が明白に異なる場合の使用は基本式の検証を要する。) | ||
| 参考とした 文献・資料 |
(社)日本騒音制御工学会・研究部会(1997)環境振動予測手法の現状と適用事例営団7号線環境影響評価書
都営12号線 新宿・練馬間及び環状部環境影響評価書 |
||
| 備考 | |||
技術シート 登録番号:振動-4
| 環境項目 | 振動 | 技術等の 種類 |
予測 |
|---|---|---|---|
| 技術等の名称 | 建設作業振動の予測(Bornizの式) | ||
| 技術等の概要 | 建設機械の作業における基準点振動レベル、振動レベルの幾何減衰係数n及び土質の内部減衰係数αから予測点における振動レベルを予測する。
L(r0)=L(r1)+20log(r1/r0)n+8.68α(r1-r0) L(r1):基準点振動レベル(dB) |
||
| 調査・対象の 必要条件 |
・建設機械の作業における基準点振動レベル
・土質条件等 |
||
| 適用範囲 | ・ 予測範囲の土質が均一
・ 振動源と受振点との間の構造的な変化がない ・ 地盤表面の性状が均一 |
||
| 課題 |
・建設機械の作業における基準点振動レベルのデータの蓄積
・ 幾何減衰定数(波動の種類:表面波、実体波、表面波と実体波の複合)や土質(シルト、ローム、砂礫、粘性土、沖積土、洪積土、岩盤等)の内部減衰定数が固定化される傾向にある。 ・ 波動の分離による減衰傾向や土質の違いによる減衰傾向の詳細な検討 ・ 地盤性状を考慮した予測の検討 ・ 振動源と受振点に介在する媒質の変化量を考慮した予測の検討 |
||
| 参考とした 文献・資料 |
塩田 正純(1986)公害振動の予測手法.井上書院、東京、pp237.
塩田 正純(1998)騒音・振動の予測手法の現状と課題.騒音制御、22(2)、88-96. |
||
| 備考 | |||
技術シート 登録番号:振動-5(1/3)
| 環境項目 | 振動 | 技術等の 種類 |
予測 |
|---|---|---|---|
| 技術等の名称 | 新幹線鉄道における統計予測式 | ||
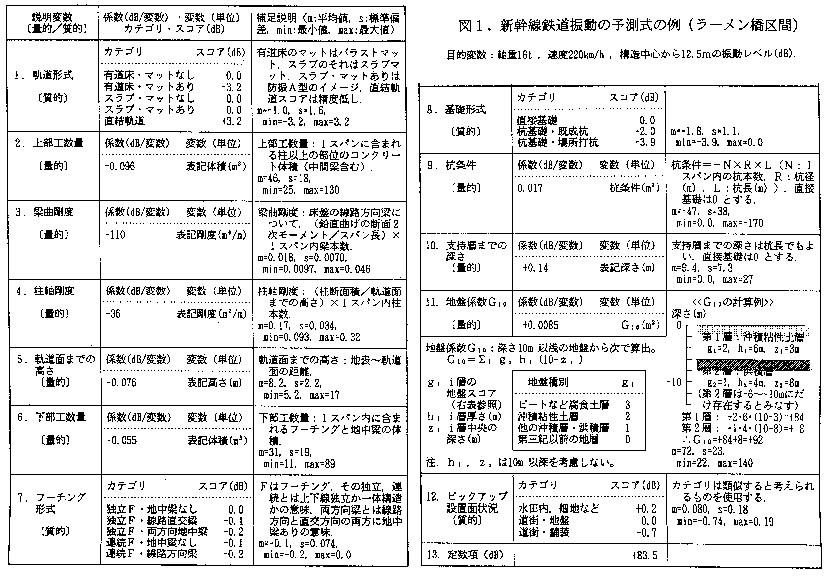
| 技術等の概要 | 新幹線鉄道振動の変動要因がどのように振動に係わるかの概略を知ることを目的として、作成された統計予測式である。予測式は以下に示すように線形回帰式を基に作成された。対象とした構造はラーメン橋及び桁橋(PC、RC桁)区間である。
L=a0+a1x1+a2x2+……+apxp L :振動レベル xj:説明変数 aj:回帰係数 なお、詳細な式等は添付資料-1に示すとおりである。 |
||
| 調査・対象の 必要条件 |
ラーメン橋の場合については添付資料-2に示すとおりである。 なお、桁橋(PC、RC桁)区間及び高架区間については、現在資料を収集中である。 |
||
| 適用範囲 |
|
||
| 課題 |
|
||
| 参考とした 文献・資料 |
(社)環境情報科学センター(1999)環境アセスメントの技術.中央法規出版、東京、pp1018.
吉岡 修(1997)環境振動予測手法を用いた適用事例-新幹線鉄道-.(社)日本騒音制御工学会・研究部会技術レポート、20、16-19. |
||
| 備考 | |||
技術シート 登録番号:振動-5(2/3)
添付資料-1
a)ラーメン橋区間
b)桁橋(PC,RC桁)区間
c)高架区間
出典;江島淳;"新幹線鉄道の桁式高架橋における地盤振動低減対策のための基礎的研究
技術シート 登録番号:振動-5(3/3)
添付資料-2
技術シート 登録番号:振動-6
| 環境項目 | 振動 | 技術等の 種類 |
予測 |
|---|---|---|---|
| 技術等の名称 | 最大速度振幅による予測(実測結果による式)[1] | ||
| 技術等の概要 | 構造物などが被害を受ける程度と良い相関を示す最大速度振幅を予測し、最大速度振幅から振動レベルを算出する予測式である。
最大速度振幅を求める式は下式に示すとおりであり、予測にあたり、K、a、bを仮定することになる。
ここで、 K :火薬類の種類や性能、発破条件、地盤条件によって決まる定数 W :雷管の段当たりの総装薬量(kg) r :爆源からの距離(m) a、b :実験(試験発破、既存データ等)により決まる定数 最大速度振幅から振動レベルを算定する式は下式に示すとおりである。
この式は、速度波形が最大速度振幅を振幅とする周波数8Hz以上の連続正弦波形(継続時間無限大)に対して成立する理論的な変換式である。 |
||
| 調査・対象の 必要条件 |
・ 発破の装薬量
・ K、a、bの定数の設定 |
||
| 適用範囲 | ・ トンネル発破
・ ベンチカット発破 ・ 得られた結果はあくまでも目安にすぎないと考える。 |
||
| 課題 | ・
環境アセスメントの段階において、現地での試験発破を実施することは困難と考える。したがって、上記の定数を採用せざるを得ない。
・ 振動レベルの変換式は、連続正弦波形(継続時間無限大)に対して成立する理論式である。したがって、発破振動波形のように継続時間の極めて短い衝撃的な振動波形に対しては、明らかに振動レベルを過大評価することになる。 |
||
| 参考とした 文献・資料 |
(社)日本騒音制御工学会技術部会・低周波音分科会(1996)発破による音と振動.山海堂、東京、pp307.
大阪府(1986)阪南丘陵開発計画に係る土砂採取事業に関する環境影響評価書. |
||
| 備考 | |||
技術シート 登録番号:振動-7(1/2)
| 環境項目 | 振動 | 技術等の 種類 |
予測 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 技術等の名称 | 最大速度振幅による予測(実測結果による式)[2] | ||||||||||||
| 技術等の概要 | 振動-5(最大速度振幅による予測(実測結果による式)[1])における振動レベルへの換算式において、振動速度波形の最大速度振幅と振動波形の継続時間から振動レベルを算出する式が提案されている。単発発破の場合の右辺第二項の0.63は振動レベル計の動特性を規定する時定数(s)を示す。
[1] 振動速度振幅の算出式 PPV=K・Wm・D-n PPV:振動速度振幅の最大値(cm/s又はkine) W:薬量(kg) D:発破源からの距離(m) K:発破係数 m:薬量に関する係数 n:距離減衰に関する係数
*:安全側をとる場合は、最も大きな値とする。 [2]振動レベルへの変換 単発発破の場合 ここにLvs :単発発破の場合の振動レベル(dB) Td :振動の継続時間 明かり発破(0.3秒)、トンネル発破(0.15秒) 段発発破の場合
ここにLv :段発発破の場合の振動レベル(dB) Ti :秒時差10~250ms(使用する雷管で決定) |
||||||||||||
| 調査・対象の 必要条件 |
振動振幅速度の算出式において、定数Kは、火薬の種類、填塞状況、穿孔等の発破条件や地盤の性質、成層状況などの要因が含まれている。より精度の高い予測値を得るためには、事前に薬量の少ない試験発破を現地で実施し、現地の状況をよりよく反映した実験式を求めることが望ましい。 | ||||||||||||
| 適用範囲 | ・ トンネル発破
・ ベンチカット発破 ・ 得られた結果はあくまでも目安にすぎないと考える。 |
||||||||||||
| 課題 | ・
環境アセスメントの段階において、現地での試験発破を実施することは困難と考える。したがって、上記の式を採用せざるを得ない。
・ ただし、同様の岩種における発破時の振動レベルデータを蓄積することによって、より精度の高い実験式を得ることが可能と考える |
||||||||||||
| 参考とした 文献・資料 |
(社)環境情報科学センター(1999)環境アセスメントの技術.中央法規出版、東京、pp1018.
(社)日本騒音制御工学会技術部会・低周波音分科会(1996)発破による音と振動.山海堂、東京、pp307. |
||||||||||||
| 備考 | |||||||||||||
技術シート 登録番号:振動-7(2/2)
添付資料-1
表-1 爆破による地盤振動伝播推定式
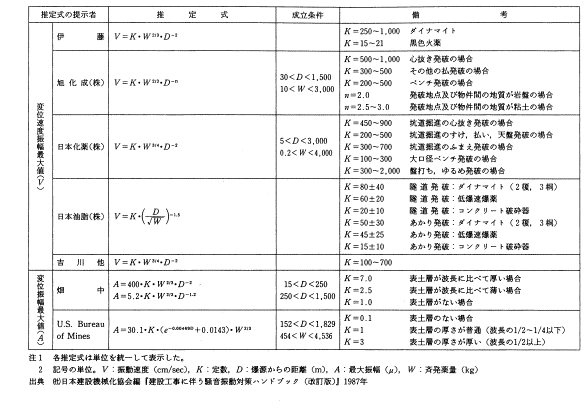
表-2 種々の現場における発破振動の段当たりの
振動速度波形の目視による継続時間
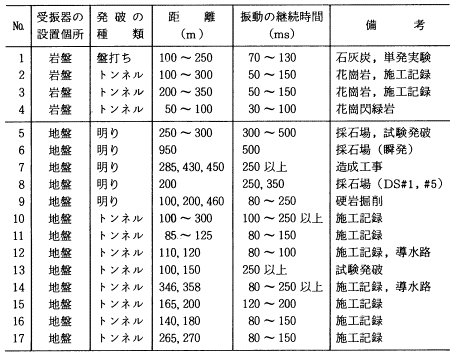
出典 (社)日本騒音制御工学会技術部会低周波音分科会(1996)
技術シート 登録番号:振動-8
| 環境項目 | 振動 | 技術等の 種類 |
評価 |
|---|---|---|---|
| 技術等の名称 | 環境振動に対する居住性能評価の動向 | ||
| 技術等の概要 |
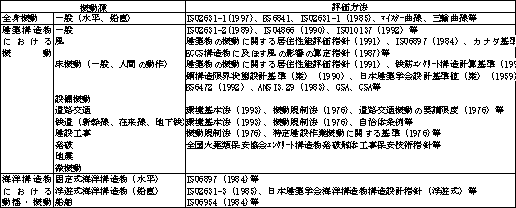
表-1 環境振動の発生源と評価方法
出典:石川孝重(2000) |
||
| 調査・対象の 必要条件 |
|||
| 適用範囲 | |||
| 課題 | |||
| 参考とした 文献・資料 |
石川考重(2000)居住性能評価の現状-第18回環境振動シンポジウム- 性能設計に向けた環境振動評価.日本建築学会環境工学委員会 環境振動小委員会.
前田節雄(2000)国際規格の動向-第18回環境振動シンポジウム- 性能設計に向けた環境振動評価.日本建築学会環境工学委員会 環境振動小委員会. |
||
| 備考 | |||
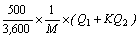
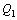 :小型車時間交通量(台/時)
:小型車時間交通量(台/時)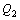 :大型車時間交通量(台/時)
:大型車時間交通量(台/時)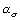 :路面の平坦性による補正値(dB)
:路面の平坦性による補正値(dB)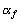 :地盤卓越振動数による補正値(dB)
:地盤卓越振動数による補正値(dB)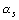 :道路構造による補正値(dB)
:道路構造による補正値(dB)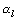 :距離減衰値(dB)
:距離減衰値(dB)